TRANS-QUÃNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.

FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =

TRANSFORMAÇÕES ⇔ INTERAÇÕES  ⇔  TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE  ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔  Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS,  ⇔   Δ MASSA ,   ⇔ Δ  CAMADAS ORBITAIS ,  ⇔  Δ FENÔMENOS  ,  ⇔  Δ  DINÂMICAS,   ⇔  Δ  VALÊNCIAS,   ⇔  Δ BANDAS,  Δ  entropia e de entalpia,  E OUTROS.  

x

 [EQUAÇÃO DE DIRAC].

 + FUNÇÃO TÉRMICA.

   +    FUNÇÃO DE RADIOATIVIDADE

  ,      +   FUNÇÃO DE TUNELAMENTO QUÂNTICO.

  + ENTROPIA REVERSÍVEL 

+      FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

 ENERGIA DE PLANCK

X

• 
  V [R] [MA] =  Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......

  ΤDCG

  X

  Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......  =
  x
  

  sistema de dez dimensões de Graceli + 

  DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
• 
  
• DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
  

  x

  sistema de transições de estados, e estados  de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].

  x

número atômico, estrutura eletrônica, níveis de energia 

[comprimento de onda (λ).

onde c, velocidade da luz, é igual a .]

• TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
• x
• X
• T l    T l     E l       Fl         dfG l   

  N l    El                 tf l

  P l    Ml                 tfefel 

  Ta l   Rl

           Ll
           D

Graus de liberdade é, na física, um termo genérico utilizado em referência à quantidade mínima de números reais necessários para determinar completamente o estado físico de um dado sistema. Esse conceito é empregado em mecânica clássica e termodinâmica.

Na mecânica, para cada partícula do sistema e para cada direção em que esta é capaz de mover-se existem dois graus de liberdade, um relacionado com a posição e outro com a velocidade. Observe-se que essa definição não coincide nem com a definição de graus de liberdade que se usa em engenharia de máquinas, nem com a que se usa em engenharia estrutural.

Mecânica clássica[editar | editar código-fonte]

Na mecânica hamiltoniana, o número de graus de liberdade de um sistema coincide com a dimensão topológica do espaço de fases do sistema. Na mecânica lagrangiana, o número de graus de liberdade coincide com a dimensão do fibrado tangente do espaço de configuração do sistema.

Mecânica estatística[editar | editar código-fonte]

Teorema de equipartição da energia[editar | editar código-fonte]

Segundo o teorema proposto por James Clerk Maxwell:

Toda molécula tem um certo número ${\displaystyle N}$ de graus de liberdade, que são formas independentes pelas quais a molécula pode armazenar energia. A cada grau de liberdade está associada (em média) uma energia de ${\displaystyle {\frac {k_{B}T}{2}}}$ 

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

por molécula (ou ${\displaystyle {\frac {RT}{2}}}$ por mol).^[1]

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

No limite clássico da mecânica estatística, a energia de uma molécula de um gás de um sistema em equilíbrio térmico com ${\displaystyle N}$ graus de liberdade quadráticos e independentes é:

${\displaystyle U=\langle E\rangle =N\,{\frac {k_{B}T}{2}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

onde:

• ${\displaystyle k_{B}}$ é a constante de Boltzmann
• ${\displaystyle T}$ é a temperatura
• ${\displaystyle N}$ é o número de graus de liberdade do sistema
• ${\displaystyle R}$ é constante universal dos gases ideais

Graus de liberdade de várias moléculas

Graus de liberdade
Moléculas	Exemplo	Translação	Rotação	Total(${\displaystyle N}$)
Monoatômicas	He, Ar, Ne, Kr	3	0	3
Diatômicas	H2, N2, O2, CO, Cl2	3	2	5
Poliatômicas	SO2, H2O, CH4	3	3	6

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Calor específico molar
Moléculas	${\displaystyle C_{v}}$	${\displaystyle C_{p}=C_{v}+R}$
Monoatômicas	${\displaystyle {\frac {3}{2}}R}$	${\displaystyle {\frac {5}{2}}R}$
Diatômicas	${\displaystyle {\frac {5}{2}}R}$	${\displaystyle {\frac {7}{2}}R}$
Poliatômicas	${\displaystyle 3R}$	${\displaystyle 4R}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

onde:

• ${\displaystyle C_{v}}$ é o calor específico molar a volume constante;
• ${\displaystyle C_{p}}$ é o calor específico molar a pressão constante

Calor específico é uma grandeza física intensiva que define a variação térmica de determinada substância ao receber determinada quantidade de calor. Também é chamado de capacidade térmica mássica. A unidade no SI é ${\displaystyle J/(kg.K)}$ (joule por quilograma e por kelvin). Uma unidade usual bastante utilizada para calores específicos é cal/(g.°C) (caloria por grama e por grau Celsius).^[1]

Em rigor há dois calores específicos distintos: o calor específico a volume constante ${\displaystyle c_{v}}$ e o calor específico a pressão constante ${\displaystyle c_{p}}$. O calor específico a pressão constante é geralmente um pouco maior do que o calor específico a volume constante, sendo a afirmação verdadeira para materiais com coeficientes de dilatação volumétrico positivos. Em virtude do aumento de volume associado à dilatação térmica, parte da energia fornecida na forma de calor é usada para realizar trabalho contra o ambiente a pressão constante e não para aumentar a temperatura em si; o aumento de temperatura experimentado para um sistema à pressão constante é pois menor do que aquele que seria experimentado pelo mesmo sistema imposto o volume constante uma vez mantida a mesma transferência de energia na forma de calor. No caso do calor específico a volume constante, toda a energia recebida na forma de calor é utilizada para elevar a temperatura do sistema, o que faz com que ${\displaystyle c_{v}}$ — em virtude de sua definição — seja um pouco menor. A diferença entre os dois é particularmente importante em gases; em sólidos e líquidos sujeitos a pequenas variações de volume frente às variações de temperatura, os valores dos dois na maioria das vezes se confundem por aproximação. Em análise teórica e de precisão, contudo, é importante a diferenciação dos dois.

Materiais com dilatação anômala, como a água entre 0 °C e 4 °C, não obedecem à regra anterior; nestes casos o calor específico a volume constante é então um pouco maior do que o calor específico a pressão constante.

Definição[editar | editar código-fonte]

O calor específico (${\displaystyle c\,\!}$) de uma substância pode ser definido a partir da capacidade térmica (${\displaystyle C\,\!}$) de um corpo composto por ela como o quociente desta pela massa (${\displaystyle m\,\!}$) desse corpo.^[2] Matematicamente,

${\displaystyle c={\frac {C}{m}}\,\!}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

A capacidade térmica, por sua vez, é definida como a razão entre calor recebido e variação de temperatura observada. Assim, o calor específico pode ser expresso como:

${\displaystyle c={\frac {1}{m}}{\frac {\delta Q}{\delta T}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Por essa última relação, nota-se que o calor específico depende do processo pelo qual o calor é cedido à substância. Usando a primeira lei da termodinâmica, com ${\displaystyle p}$ sendo a pressão, pode-se escrever:

${\displaystyle c={\frac {1}{m}}{\frac {\mathrm {d} U+p\mathrm {d} V}{\mathrm {d} T}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Dois casos particulares são de maior importância. Um deles é o calor específico a volume constante, onde o termo representando o trabalho (${\displaystyle p\mathrm {d} V}$) é nulo, e pela relação anterior

${\displaystyle c_{v}={\frac {1}{m}}{\frac {\mathrm {d} U}{\mathrm {d} T}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

O segundo caso é o calor específico a pressão constante. Nesse caso, a equação anterior resulta em

${\displaystyle c_{p}={\frac {1}{m}}{\frac {\mathrm {d} \left(U+pV\right)}{\mathrm {d} T}}}$,

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

onde a nova função de estado ${\displaystyle H=U+pV}$ é entalpia do sistema.^[3]

A distinção entre esses dois calores específicos pode normalmente ser ignorada nas fases sólida e líquida, dado que essas substâncias normalmente sofrem uma variação de volume muito pequena. Gases, no entanto, apresentam grande expansão térmica, sendo sempre necessária a distinção entre ambos os calores específicos.

Calor específico molar[editar | editar código-fonte]

Em muitas circunstâncias a unidade mais conveniente para especificar a quantidade de uma substancia é o mol, definido como sendo uma quantidade de 6,02 x 10²³ unidades elementares de qualquer substância. Assim, por exemplo um mol de alumínio significa 6,02 x 10²³ átomos de alumínio (o átomo é a unidade elementar), e 1 mol de óxido de alumínio significa 6,02 x 10²³ fórmulas moleculares do composto.

Nesses casos, quando a quantidade de substância é expressa em moles, utiliza-se o chamado calor específico molar, que é expresso como sendo a capacidade térmica por mol.^[4] De forma análoga com o calor específico por massa, o calor específico molar depende do processo ao qual a substância é submetida; define-se de mesma forma as quantidades a pressão constante e a volume constante.

Calor específico molar a volume constante[editar | editar código-fonte]

O calor específico molar a volume constante é definido como:

${\displaystyle c_{v}={\frac {Q}{n\Delta T}}={\frac {\Delta U}{n\Delta T}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Sendo que,

${\displaystyle \Delta U=Q-W}$ (primeira lei da termodinâmica) com o trabalho ${\displaystyle W=0}$ temos ${\displaystyle \Delta U=Q}$,por se tratar de um processo a volume constante.

onde:

• ${\displaystyle Q}$ é o calor absorvido ou cedido por uma amostra de ${\displaystyle n}$ moles de um gás;
• ${\displaystyle \Delta T}$ é a variação de temperatura resultante;
• ${\displaystyle \Delta U}$ é a variação de energia interna.

Para um gás monoatômico ideal,

${\displaystyle c_{v}={\frac {3}{2}}R=12,5J/mol/K}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Calor específico molar a pressão constante[editar | editar código-fonte]

O calor específico molar a pressão constante é definido como:

${\displaystyle c_{p}={\frac {Q}{n\Delta T}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Sendo que temos as seguintes relações:

${\displaystyle Q=U+W}$ (primeira lei da termodinâmica) e ${\displaystyle W=p\Delta V}$. Relacionando o trabalho com a equação dos gases ideais ${\displaystyle pV=nRT}$ ficamos com ${\displaystyle W=nR\Delta T}$. Substituindo a as respectivas equações mais a equação ${\displaystyle c_{v}={\frac {\Delta U}{n\Delta T}}}$ na equação ${\displaystyle Q=U+W}$ ficamos com

${\displaystyle c_{p}=c_{v}+R}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

onde:

• ${\displaystyle Q}$ é o calor absorvido ou cedido por uma amostra de ${\displaystyle n}$ mols de um gás;
• ${\displaystyle \Delta T}$ é a variação de temperatura resultante;
• ${\displaystyle \Delta U}$ é a variação de energia interna.

Regra de Dulong-Petit[editar | editar código-fonte]

A regra de Dulong-Petit consiste em obter, aproximadamente, o calor específico das substâncias por meio da massa molar:

${\displaystyle c\cong {\frac {3R}{M}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Em que:

• ${\displaystyle c}$ é o calor específico, em joule por quilograma kelvin (J.kg⁻¹.K⁻¹);
• ${\displaystyle R}$ é a constante dos gases reais, equivalente a 8,31 joules por mol kelvin (J.K⁻¹.mol⁻¹);
• ${\displaystyle M}$ é a massa molar, em quilograma por mol (kg/mol).

Unidades[editar | editar código-fonte]

Sistema internacional[editar | editar código-fonte]

A unidade SI para calor específico é joule por kelvin por quilograma (J / K / kg, J / (kg K), JK ^-1 kg ^-1 , etc.). Como um incremento de temperatura de um grau Celsius é o mesmo que um incremento de um kelvin, é o mesmo que joule por grau Celsius por quilograma (J / ° C / kg). Às vezes, o grama é usado em vez de quilograma para a unidade de massa: 1 J / K / kg = 0,001 J / K / g.

O calor específico de uma substância (por unidade de massa) tem dimensão L ² · T − ² · Θ ⁻¹ ou (L / T) ² / Θ. Portanto, a unidade SI J / K / kg é equivalente ao metro quadrado por segundo ao quadrado por kelvin (m ² K ⁻¹ s ⁻² ).

Unidades de engenharia inglesas (imperiais)[editar | editar código-fonte]

Profissionais da construção , engenharia civil , engenharia química e outras disciplinas técnicas, especialmente no Estados Unidos , pode utilizar os chamados unidades de Inglês Engenharia , que incluem a imperial libra (lb = 0,45459237 kg) como unidade de massa, o grau Fahrenheit ou Rankine (° F = 5/9 K, cerca de 0,555556 K) como a unidade de incremento de temperatura, e a unidade térmica britânica (BTU ≈ 1055.06 J), ^[5] [6] como a unidade de calor.

Medição do calor específico de uma substância[editar | editar código-fonte]

Calorímetro

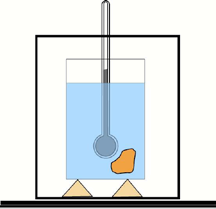
A capacidade calorífica de um corpo é determinada com ajuda de um calorímetro e um termômetro. Um calorímetro simples (veja a figura) consiste num cilindro metálico polido, colocado num outro cilindro metálico sobre cortiça (para isolamento térmico).^[7]

O calor específico de uma substância é normalmente determinado de acordo com a definição; ou seja, medindo a capacidade térmica de uma amostra da substância, geralmente com um calorímetro , e dividindo pela massa da amostra. Várias técnicas podem ser aplicadas para estimar a capacidade térmica de uma substância como, por exemplo, calorimetria de varredura diferencial rápida . ^[8] [9]

O cilindro interno é enchido com água ou algum outro líquido de calor específico conhecido. Um corpo de massa m, e capacidade calorífica específica c, aquecido a uma certa temperatura T é imergido no calorímetro de massa m₁ e capacidade calorífica c₁ na qual a temperatura é medida. Suponha que a temperatura deste líquido de m₂ e capacidade calorífica específica c₂ no calorímetro é T’ antes de o corpo ser emergido nele, e quando a temperatura do líquido e do corpo é a mesma, a temperatura torna-se T_f.

Da lei de conservação da energia e considerando o calor dissipado na vizinhança pelo objecto quente Q, o calor recebido pela água e pelo calorímetro que seja respectivamente Q₁ e Q₂ , mostra que a capacidade calorífica específica é

${\displaystyle c={\frac {c_{1}m_{1}(T_{f}-T)+c_{2}m_{2}(T_{f}-T')}{m(T-T_{f})}}={\frac {(c_{1}m_{1}+c_{2}m_{2})(T_{f}-T')}{m(T-T_{f})}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS 

Fatores que afetam o calor específico[editar | editar código-fonte]

Representação de uma molécula vibrando.

Moléculas sofrem muitas vibrações características internas. A energia potencial armazenada nestes graus de liberdade internos contribui para uma amostra do conteúdo de energia, mas não a sua temperatura. Graus de liberdade mais internos tendem a aumentar a capacidade de uma substância de calor específico, contanto que as temperaturas são suficientemente elevadas para superar os efeitos quânticos.

Graus de liberdade[editar | editar código-fonte]

O comportamento termodinâmico das moléculas dos gases monoatômicos, como hélio, e dos gases diatômicos, como o nitrogênio, é muito diferente. Em gases monoatômicos, a energia interna é unicamente para movimentos de translação. Os movimentos são movimentos de translação em um espaço tridimensional em que as partículas se movem e trocam energia em colisões elásticas da mesma forma como fariam bolas de borracha colocadas num recipiente que foi agitado fortemente. (Veja animação aqui). Estes movimentos nas dimensões X, Y, e Z significam que os gases monoatômicos tem apenas três graus de liberdade de translação. Moléculas com maior atomicidade, no entanto, tem vários graus de liberdade interna, rotacionais e vibracionais. Elas se comportam como uma população de átomos que podem se mover dentro de uma molécula de formas diferentes (veja a animação à direita). A energia interna é armazenada nesses movimentos internos. Por exemplo, o nitrogênio, que é uma molécula diatômica, tem cinco graus de liberdade: três de translação e dois de rotação interna. Note que a calor específico molar a volume constante do gás monoatômico é ${\displaystyle {\frac {3}{2}}R}$, sendo R a constante universal do gás ideal, ao passo que para o valor do nitrogênio (diatômico) vale ${\displaystyle {\frac {5}{2}}}$, o que mostra claramente a relação entre os graus de liberdade e ao calor específico.

${\displaystyle c_{v}=({\frac {f}{2}})R}$ onde ${\displaystyle f}$ é o número de graus de liberdade.

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS